Modeling the problem
The E1CRP introduced in the previous section takes advantage of a particular structure that is exploited through its representation in a suitable graph. A graph is a mathematical object constituted by a set N of nodes and a set A of pairs of nodes called arcs. In particular here we consider ordered pairs of nodes, therefore the graph is said to be directed. Notice that such a graph does not correspond to the physical network since the nodes model actions rather than physical places.
Let be {1,…, n} the service requests. Each request i is characterized by a material type μi, a container type Βi, and a RDS γi. Two requests are called be compatible if they use the same container type.
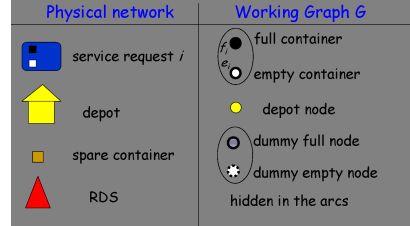Nodes of graph G are associated to the requests, in particular two nodes fi(
) and ei(
) correspond to each request i: they represent the actions of bringing the full container to a disposal plant for material μi, and of taking an empty container of type Βi, to γi in order to replace the full one, respectively. Set N also includes node d as the depot.
Notice that the MRFs are not explicitly represented by nodes since they will be embedded in the arcs.
The arc set A can be partitioned into two classes of arcs. Loaded arcs (
) model vehicles activities when loaded with a container, either full or empty, while unloaded arcs (
) model any vehicle trip without container.
Loaded arcs connect fi to ej for any pair of compatible requests i and j such that the duration of the sequence of actions denoted by the nodes d, fi, ei, d does not exceed the maximum duration.
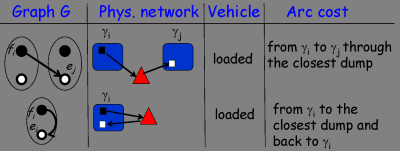
Arc (fi, ei) models the following sequence of actions: transporting the full container of i from γi to a disposal plant for material μi emptying the container, transporting it to γj and unloading it there.
Notice that the disposal plant is selected as the one on the cheapest detour from γi to γj. Disposal plants are thus embedded into loaded arcs, whose costs includes travel times, dumping and unloading times. If i = j, arc (fi, ei) models the so called petal pattern, i.e., bringing back a container to its original site once emptied.
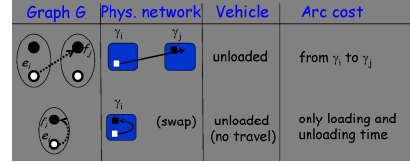Unloaded arcs connect ei to fj, for any pair of requests i and j, regardless of container types.
Arc (ei, fj) models a vehicle that travels unloaded from γi up to γj where it picksup the full container of request j. Its cost includes the travel time from γi to γj , plus container loading time. Note that the arc is defined only given that its duration plus the travel time from d to γi and from γj to d passing by the closest MRF, does not exceed the maximum duration.
If γi = γj and βi = βj, an arc is said co-sited: co-sited unloaded arcs have a null trip and model the swap pattern, i.e., bringing an empty container to a site and swap it with a compatible full one.
This is the only pattern followed by the GESENU company, but has the disadvantage of constraining the vehicle to a given container type and of requiring the detour through the depot in order to change container type.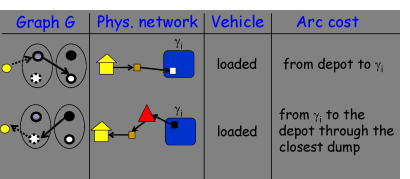
So far, a vehicle must leave and return to the depot unloaded. Whereas the availability of spare containers at the depot allows to deliver an empty container as a first action, or to return to the depot just after a dumping action with the vehicle loaded by an empty container. Spare containers are modeled by way of pairs of dummy nodes dfi (
) and dei (
) corresponding to the action of taking an empty container at the depot and of returning it, respectively.
Every arc of the graph described, represent an operation that can be performed by a single vehicle.
Since we deal with both minimum total duration and minimum fleet size our algorithm operates at two different levels of granularity: tours and routes. A tour is an elementary cycle by d and a route is a sequence of tours. A route is said feasible if its duration does not exceed the maximum one allowed for a vehicle.
The problem stated on graph G can be interpreted as a particular case of the Vehicle Routing Problem (VRP) with an additional constraint on the duration of each vehicle and no constraint on capacity. Indeed, the 1-load constraint is modelled by the graph topology. The peculiar structure of G (the graph is bipartite) allows as to taylor solution approaches that exploit it.
Solving the problem
In order to minimize the total travel time of all vehicles we explore different way of sequencing nodes into tours, whereas in order to minimize the fleet size we explore different way of packing tours into routes.
The first goal is obtained by way of moves which constitute the base of a Tabu Search framework. A move is a change in a solution that transforms a feasible solution into another one.
For instance the figure below depicts a inter-tour move, called string cross and relocation of unloaded arcs, consisting in the swap of two sequences of arcs of two different tours (ta and tb) by deleting the four unloaded arcs that precede or follow each sequence, by inserting each of them into the other tour and reconnecting each of them in the only possible way (without reversing) through the insertion of four new unloaded arcs.
The Tabu Search (see http://www.cs.colostate.edu/~whitley/CS640/hertz92tutorial.pdf for a tutorial) is a metaheuristic algorithm that exploits the moves for generating a sequence of solutions from an initial starting one. Such framework substantially differs from the Local Search algorithm since once a local optimum is found it tries to obtain a better one by continuing the Local Search forbidding (for this the name Tabu Search) some moves that otherwise will yield the same solution.
The second goal, i.e. packing tours into routes, is obtained by way of an algorithm for the bin packing problem (BPP): given a set of items with known size and an unbounded set of bins with fixed capacity, the BPP consists in assigning the items to the bin so to minimize the number of bins employed. In our case the items are represented by the tours (the size is their duration) and the bins are represented by the routes (the capacity is the maximum travel time allowed to a vehicle).
Since BPP cannot be solved to optimality in reasonable time we have to content with a heuristic algorithm i.e. with a procedure that can just to guarantee of finding a “good” feasible solution, but not necessarily the optimal one. In particular we use the so called best fit decreasing algorithm (see http://www.or.deis.unibo.it/kp/Chapter8.pdf ) slightly adapted to our context.
Software tool and impact on GESENU company
The algorithm has been implemented and included in a software tool with an user friendly interface.
In most critical cases the software tool allowed GESENU to use 2 vehicles instead of 3, thus saving about 1/3 of the operational cost.
