Alberi finiti

L'insieme Tree degli alberi finiti si definisce induttivamente come segue:

EmptyTree: Tree (l'albero vuoto);
se k >= 0 e t_1, ... , t_k: Tree allora ConsTree(t_1, ... , t_k): Tree

In parole gli alberi finiti sono generati a partire dall'albero vuoto dall'operazione finitaria ConsTree che ha per argomento una sequenza finita ed evenutalmente vuota di sottoalberi finiti. In particolare ConsTree() è l'albero formato da un solo nodo.

Volendo etichettare i vertici dell'albero con elementi da un certo insieme T si può modificare la seconda clausola premettendo un argomento di tipo T nella definizione di ConsTree:

EmptyTree: Tree(T);
se a:T e k >= 0 e t_1, ... , t_k: Tree(T) allora ConsTree(a,t_1, ... , t_k): Tree(T).

Realizzazione di alberi con il vettore dei padri

Questa realizzazione presuppone che sia noto un confine superiore alla cardinalità dell'albero, cioè al numero dei vertici in un albero. Un albero è rappresentato da un vettore i cui elementi sono associati ai vertici e contengono l'informazione sull'indice del padre di ciascun vertice (-1 nel caso della radice).

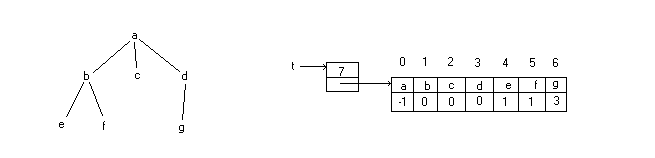
Nell'esempio l'albero è rappresentato da un puntatore ad un record che contine l'informazione sulla cardinalità, ed un puntatore al vettore che associa i figli ai padri. In questo vettore, ad esempio, il vertice con etichetta g è associato al vertice di indice 3 che ha etichetta d, perché questo vertice è il padre di g.

Si utilizzi la seguente dichiarazione di tipo:

typedef struct treevertex {
    T VLabel;  // etichetta del vertice
    int Father; // indice del vertice padre
} TreeVertex; // tipo degli elementi del vettore dei vertici

typedef struct treevec {
    int Card;  // cardinalita' dell'albero
    TreeVertex* VertexVec; // puntatore al vettore dei vertici
} TreeVec; // tipo della coppia (cardinalita', vettore dei vertici)

typedef TreeVec* TreeT; // tipo degli alberi finiti

Concepire e realizzare un'implementazione degli alberi finiti con questa tecnica; per sperimentarla si scriva quindi il codice della coppia di funzioni:

TreeT ReadTree(String s); 
/* trasforma la rappresentazione parentesizzata s di un albero
nel vettore dei padri */

void WriteTree(Tree t);
/* stampa il vettore dei vertici in forma di una successione di coppie
   (etichetta, indice del padre)  */

dove la rappresentazione parentesizzata degli elementi di Tree(T) è definita:

() =  EmptyTree
(a t_1 ... t_k) = ConsTree(a,t_1, ... , t_k)

Nota: il vantaggio di questa realizzazione è che in realtà possiamo utilizzarla per foreste (insiemi finiti di alberi) invece che per singoli alberi. Gli svantaggi sono una notevole rigidità (non si possono sempre aggiungere vertici ad alberi preesistenti) ed un'implementazione inefficiente delle routine di visita.

Soluzione.

Realizzazione dinamica di alberi n-ari

Una specifica dell'ADT Tree(T) è la seguente:

datatype       Boolean, Nat, T, Tree(T);
constructors:  EmptyTree: Tree(T);
               ConsTree: T, Tree(T)^* -> Tree(T);
observations:  IsEmptyTree: Tree(T) -> Boolean;
               Label: Tree(T) -> T;
               SubTree: Nat, Tree(T) -> Tree(T);
equations:     IsEmptyTree(EmptyTree) = True;
               IsEmptyTree(ConsTree(a,t_1, ... , t_k)) = False;
               Label(ConsTree(a,t_1, ... , t_k)) = a;
               i <= k ==> SubTree(i,ConsTree(a,t_1, ... , t_k)) = t_i;
               i > k ==> SubTree(i,ConsTree(a,t_1, ... , t_k)) = EmptyTree;

dove A^* rappresenta l'insieme delle sequenze finite di oggetti in A.

Esercizi

Si realizzi un'implementazione degli alberi binari con la tecnica dei puntatori.
Si realizzi un'implementazione dell'ADT Tree(T) utilizzando la seguente codifica di alberi n-ari in alberi binari: ad ogni vertice dell'albero dato è associato un vertice dell'albero binario il cui campo left punta alla lista di sottoalberi, ed il cui campo right punta alla lista degli fratelli (dello stesso livello).

Quindi si riscriva il codice della coppia di funzioni (badando alla nuova forma di WriteTree):
```
TreeT ReadTree(String s); 
/* trasforma la rappresentazione parentesizzata s di un albero
nell'albero binario che ne codifica la struttura */

void WriteTree(Tree t, String s);
/* scrive in s la rappresentazione parentesizzata di t*/
```