Insiemi disgiunti

L'ADT degli insiemi disgiunti

Sia S un insieme: una partizione finita di S è una famiglia finita di sottoinsiemi di S tale che S sia l'unione della famiglia, ed i membri della famiglia siano due a due disgiunti. Una partizione induce un concetto di equivalenza tra gli elementi di S: x equivale a y se entrambi appartengono allo stesso insieme della partizione. Nel seguito ogni insieme della partizione, ovvero ogni classe d' equivalenza, sarà associato ad un elemento che gli appartiene (si assume che S sia non vuoto e che tali siano gli insiemi della partizione), detto il suo rappresentante.

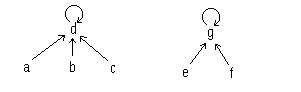
L'ADT degli insiemi disgiunti è così specificato:

datatype Disjoint_Set, Set, T;

constructors: Create: Set -> Disjoint_Set;
              Union: Disjoint_set,T,T -> Disjoint_Set;
			  
observation:  Find: Disjoint_Set,T -> T;

semantics: Create(S) ritorna la partizione di S in cui ogni insieme e' un singoletto
           Union(D,x,y) ritorna la partizione che si ottiene da D rimpiazzando
                        gli insiemi di cui x e y sono rappresentanti con la loro unione
           Find(D,a) ritorna il rappresentante dell'insieme in D cui a appartiene,
                     se esiste; un valore nullo altrimenti.

Una possibile realizzazione di questo ADT fa uso di una foresta di alberi realizzati con la tecnica del vettore dei padri (detti anche up-trees, perché ogni vertice punta al suo predecessore invece che ai suoi successori). Ad esempio l'insieme S={a,b,c,d,f} partizionato in D={{a,b,c,d},{e,f,g}} lo possiamo rappresentare con la foresta:

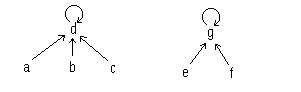
in cui gli elementi in radice, d,g, rappresentano i due insiemi della partizione. L'operazione union(D,d,g) trasforma questa partizione nella partizione {{a,b,c,d,e,f,g}}, ottenuta, ad esempio, facendo diventare g un figlio di d:

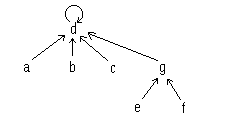
In questo modo il costo in tempo dell'unione è O(1). Lasciando indeterminato il criterio per cui si è scelto di rendere g figlio di d e non viceversa, successive operazioni di unione possono trasformere la foresta che rappresenti la partizione triviale (in singoletti) in un albero degenere, su cui l'operazione find avrebbe costo O(n). Si può invece ottenere che il tempo di find sia molto prossimo ad O(1) (un buon confine superiore è O(m lg^* n) dove lg^* è la funzione logaritmica iterata, m è il numero di operazioni compiute a partire dalla partizione iniziale, ed n è la cardinalità dell'insieme partizionato).

Il metodo per ottenere questo risultato combina due euristiche (Cormen et alii. cap. 22):

Unione per rango. Ad ogni vertice si associa un rango, ossia un confine superiore all'altezza del sottoalbero che ha radice nel vertice. Nella partizione iniziale ogni vertice ha rango 0. Quando si esegue union(D,x,y), se rango(x) <= rango(y) allora x diventa figlio di y e rango(y) si incrementa di 1; altrimenti y diventa figlio di x.
Compressione del cammino. Nel cercare la radice dell'albero che contiene il vertice a, find(D,a) risale lungo un ramo incontrando una sequenza finita di vertici, detta il find path di a in D; la compressione consiste nel rendere tutti i vertici del find path figli della radice dell'albero in cui sono.

Esercizio. Si implementi l'ADT Disjoint_Set usando le euristiche dell'unione per rango e della compressione del cammino integrando il file InsDisTest.java. Questo realizza una foresta di alberi di arietà variabile con il cosiddetto metodo del "vettore dei padri".

Questa realizzazione presuppone che sia noto un confine superiore alla cardinalità dell'albero, cioè al numero dei vertici in un albero. Un albero è rappresentato da un vettore i cui elementi sono associati ai vertici e contengono l'informazione sull'indice del padre di ciascun vertice (-1 nel caso della radice).

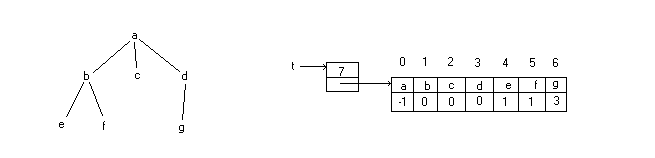
Nell'esempio l'albero è rappresentato da un puntatore ad un record che contine l'informazione sulla cardinalità, ed un puntatore al vettore che associa i figli ai padri. In questo vettore, ad esempio, il vertice con etichetta g è associato al vertice di indice 3 che ha etichetta d, perché questo vertice è il padre di g.

Nulla impone, tuttavia, che il vettore rappresenti una struttura connessa, cioè un solo albero: in generale la stessa tecnica consente di realizzare una foresta, ossia un insieme di alberi, nota la somma delle cardinalità. In questo caso le radici degli alberi sono contraddistinte dal fatto di avere -1 come indice al padre.