Geometria.nb

Esercizio 7 del Capitolo 1 (Abbena-Gianella).

Risolvere il sistema nel parametro a:

a x1 - x2 + x3 = 2

x1 - x2 + a x3 = a + 1

Suggerimenti. Ripulire (col comando Clear) la variabile a. Quindi definire una matrice A dei coefficienti, due vettori (cioè due liste) X delle variabili e B dei coefficienti. Disegnare per controllo A, X, A.X, B (usare MatrixForm).

In[282]:=

In[283]:=

A = { {a, -1, 1}, &nbs ... br /> {1, -1, a} } ;

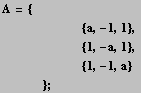
In[284]:=

In[285]:=

$B = {2, 3 - a^2, a + 1} ;$

In[286]:=

MatrixForm[A] MatrixForm[X] MatrixForm[A . X] MatrixForm[B]

Out[286]//MatrixForm=

Out[287]//MatrixForm=

Out[288]//MatrixForm=

Out[289]//MatrixForm=

Calcolare il determinante, e scoprire per quali valori di A risulta Det[A]=0. Per tali valori di a, le soluzioni potranno essere più di una.

In[290]:=

Out[290]=

In[291]:=

Out[291]=

Infine, calcolare la soluzione di A.X=B in generale, e per i valori di a per cui Det[A]=0. Solve fornisce la soluzione generale vale solo quando Det[A] è diverso da 0. Reduce fornisce anche le soluzioni per i particolari valori di a che rendono il determinante nullo. Anzichè usare Reduce, si può risolvere l'equazione Det[A] == 0, quindi ricalcolare le soluzioni di AX=B e la forma ridotta di A, per stabilire, in questi casi, la dimensione dello spazio delle soluzioni.

In[292]:=