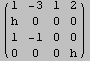
determinare per quali valori di h è invertibile, e in questi casi scrivere l'inverso di A.
Capitolo 2. Matrici e Determinanti.
Esercizio 4, Capitolo 2 (Abbena-Gianella). Data la matrice A nel parametro h:
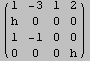
determinare per quali valori di h è invertibile, e in questi casi scrivere l'inverso di A.
Suggerimenti. Ripulire (col comando Clear) la variabile h. Definire una matrice A e disegnarla per controllo (usare MatrixForm). Risolvere l'equazione (in h) Det[A]=0.
In[300]:=
![]()
In[301]:=
![A = {<br /> {1, -3, 1, 2}, <br /> {h, 0, 0, 0} ... sp; {1, -1, 0, 0}, <br /> {0, 0, 0, h}} ; MatrixForm[A]](../HTMLFiles/index_46.gif)
Out[302]//MatrixForm=
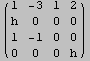
In[303]:=
![]()
Out[303]=
![]()
In[304]:=
![]()
Out[304]=
![]()
La matrice risulta invertibile per i valori di h diversi da quelli trovati sopra. Usando il comando Inverse possiamo calcolare la formula per la matrice inversa (esistente, però, solo quando Det[A] è diverso da 0).
In[305]:=
![]()
Out[306]//MatrixForm=
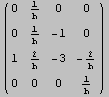
Esercizio 15, Capitolo 2 (Abbena-Gianella). Data la matrice rettangolare e i vettori:
A = ![]() , X =
, X = ![]()
B1 = ![]() , B2 =
, B2 = ![]() , B3 =
, B3 = ![]()
discutere e risolvere le equazioni AX=B1, AX=B2, AX=B3.
Suggerimenti. Ripulire x1, x2, x3, x4, e definire la matrice A e i vettori (liste) B, B1, B2, B3, controllando con MatrixForm i dati inseriti.
In[307]:=
![]()
In[308]:=
![A = {<br /> {2, -3, -2, 1}, <br /> ... , 0} ; MatrixForm[A] MatrixForm[A . X] MatrixForm[X] MatrixForm[B1] MatrixForm[B2] MatrixForm[B3]](../HTMLFiles/index_60.gif)
Out[313]//MatrixForm=
![]()
Out[314]//MatrixForm=
![]()
Out[315]//MatrixForm=
![]()
Out[316]//MatrixForm=
![]()
Out[317]//MatrixForm=
![]()
Out[318]//MatrixForm=
![]()
Lo spazio delle soluzioni (qualora non sia vuoto), per matrici rettangolari ha dimensione pari al numero delle variabili (4, in questo caso) meno il rango (il numero di righe non tutte nulle) della forma ridotta di A. Calcoliamolo usando il comando RowReduce, che ci dà la forma ridotta di una matrice:
In[319]:=
![]()
Out[319]//MatrixForm=
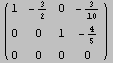
La dimensione dello spazio delle soluzioni (sempre qualora non sia vuoto) si può alternativamente calcolare come la lunghezza di una base dello spazio delle soluzioni di AX=0. Una tale base si può generare con il comando NullSpace, applicato alla matrice A.
In[320]:=
![]()
Out[320]//MatrixForm=
![]()
Out[321]=
![]()
Risolviamo ora le equazioni AX = B1, B2, B3, e notiamo che lo spazio delle soluzioni (quando non è vuoto) ha sempre la soluzione calcolata in precedenza. Non c'è differenza, in questo caso, tra le risposte ottenute con Solve e Reduce, tranne che nella forma. Per esempio, AX=B1 non ha soluzioni. Quindi Solve ci risponderà {} (lista vuota di condizioni), mentre Reduce ci risponderà False (la costante logica che definisce appunto l'insieme vuoto).
In[322]:=
![]()
Out[322]=
![]()
Out[323]=
![]()
In[324]:=
![]()
![]()
Out[324]=
![]()
Out[325]=
![]()
In[326]:=
![]()
![]()
Out[326]=
![]()
Out[327]=
![]()
Created by Mathematica (August 4, 2004)