Esercizi sui sottospazi.

Esercizio 2, Cap.4 (Abbena-Gianella). Siano dati i vettori:
    u1 = (1,-1,0,1)
    u2 = (2,1,1,0)
    u3 = (3,0,1,1)                
    u4 = (0,1,-1,0)
Trovare una base del sottospazio S da essi generato. Verificato che u1,u2,u4 sono linearmente indipendenti, determinare per quali valori di un parametro t il vettore v=(1,-1,2t-8,t+1) appartiene ad S.

Suggerimenti. Non dimenticate di ripulire la variabile t, e di definire i vettori come liste.

In[355]:=

Clear[t, l1, l2, l3]

In[356]:=

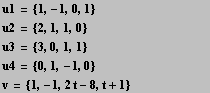
u1 = {1, -1, 0, 1} u2 = {2, 1, 1, 0} u3 = {3, 0, 1, 1}              u4 = {0, 1, -1, 0} v = {1, -1, 2t - 8, t + 1}

Out[356]=

{1, -1, 0, 1}

Out[357]=

{2, 1, 1, 0}

Out[358]=

{3, 0, 1, 1}

Out[359]=

{0, 1, -1, 0}

Out[360]=

{1, -1, -8 + 2 t, 1 + t}

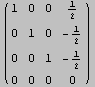
Verifichiamo (calcolando la forma ridotta) che {u1,u2,u3,u4} sono linearmente dipendenti, mentre {u1,u2,u4} no.

In[361]:=

RowReduce[{u1, u2, u3, u4}]//MatrixForm

Out[361]//MatrixForm=

( 1 ) - 1 0 0 2 ... 1 -- 0 0 1 2 0 0 0 0

In[362]:=

RowReduce[{u1, u2, u4}]//MatrixForm

Out[362]//MatrixForm=

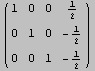
( 1 ) - 1 0 0 2 ... 1 0 2 1 -- 0 0 1 2

Troviamo un valore di t per cui v = l1*u1+l2*u2+l3*u4 per qualche l1,l2,l3.

In[363]:=

Solve[v == l1 * u1 + l2 * u2 + l3 * u4]

Out[363]=

{{l13, l2 -1, l33, t2}}

Esercizio 3, Cap.4 (Abbena-Gianella). Siano dati i vettori:
    u = (1,3,2)
    v = (-2,1,1)
Trovare una base del sottospazio S da essi generato. Verificato che u, v sono linearmente indipendenti, determinare per quali valori di un parametro t il vettore w=(t,0,-1) appartiene ad S.
Disegnate u, v, w ed il sottospazio S.

Suggerimenti. Non dimenticate di ripulire la variabile t, e di definire i vettori come liste.

In[364]:=

Clear[t, l1, l2]

In[365]:=

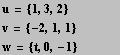
u = {1, 3, 2} <br />v = {-2, 1, 1} <br />w = {t, 0, -1}     

Out[365]=

{1, 3, 2}

Out[366]=

{-2, 1, 1}

Out[367]=

{t, 0, -1}

Verifichiamo (calcolando la forma ridotta) che {u,v} sono linearmente indipendenti.

In[368]:=

RowReduce[{u, v}]//MatrixForm

Out[368]//MatrixForm=

( 1 ) -- 1 0 7 5 - 0 1 7

Troviamo un valore di t per cui w = l1*u+l2*v per qualche l1,l2.

In[369]:=

Solve[w == l1 * u + l2 * v]

Out[369]=

{{l11, l2 -3, t7}}

In[370]:=

t = 7 ; w

Out[371]=

{7, 0, -1}

Per disegnare vettori in 3D scaricate (se non l'avete già fatto) il file MathMacro.txt contenente il comando
                    Arrow3D[{x,1,x2,x3},"etichetta"]
L'indirizzo è:
          http://www.di.unito.it/~stefano/MathMacro.txt
Inserite il file nella cartella in cui lavora Mathematica (per sapere qual'è, date il comando Directory[]). Caricate il file con il comando entro Mathematica:
                                  <<MathMacro.txt

In[372]:=

<<MathMacro.txt

INDICE MATHMACRO.TXT            &n ... aseHelp, eccetera. Scrivere MathMacroHelp per leggere tutte le istruzioni in ordine alfabetico. \n

Disegnamo ora u,v, w con un grafico (di nome g).

In[373]:=

RowBox[{RowBox[{ConeRadius, , =, , 0.3}], ;}] g = Show[<br />    Arrow3D ... <br />    ImageSize->700] RowBox[{RowBox[{ConeRadius, , =, , 0.1}], ;}]

[Graphics:../HTMLFiles/index_156.gif]

Out[374]=

⁃Graphics3D⁃

Disegnamo S, lo spazio vettoriale generato da u, v. Per definizione, S = {l1*v+l2*u|l,mεR}. E' quindi sufficiente disegnare S come grafico 3D parametrico di (l1*v+l2*u), dipendente dai parametri l1, l2 (comando ParametricPlot3D[...]).
Ripulite prima l1,l2. Date ad l1, l2 un intervallo di valori che comprenda sia 0, 1, sia le soluzioni di w = l1*u + l2*v viste in precedenza.

In[376]:=

Clear[l1, l2]

In[377]:=

g ' = ParametricPlot3D[l1 * u + l2 * v, {l1, 0, 1}, {l2, -3, 1}]

[Graphics:../HTMLFiles/index_160.gif]

Out[377]=

⁃Graphics3D⁃

Sovrapponiamo ora il disegno g di u,v,w con il disegno g' di S (comando Show[g,g']).

In[378]:=

Show[g, g ']

[Graphics:../HTMLFiles/index_163.gif]

Out[378]=

⁃Graphics3D⁃

Created by Mathematica  (August 4, 2004)