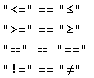
Evaluating atomic formulas.

Take any string S representing some atomic formula. We want to compute the truth value of S, or decide that S is an open formula without a fixed truth value. We first replace round brackets by square brackets, because Mathematica notation requires square brackets. We replace <=, >=, ==,!= with the special symbols ≤, ≥, ==,≠. These special symbols are considered, in Mathematica,  different from <=, >=, ==,!=, as we check below:

In[91]:=

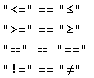
Out[91]=

Out[92]=

Out[93]=

Out[94]=

Then every = not occurring in some <=, >=, = =, != in S is replaced by the special symbol ==.

In[95]:=

Eventually we can evaluate S, or decide it has no fixed truth value, using ternary ``if'' of Mathematica. If S is neither true nor false, we say that the truth value of S is open.

In[96]:=

Some examples.

In[97]:=

In[98]:=

Out[98]=

In[99]:=

Out[99]=

In[100]:=

Out[100]=

Mathematica can recognize some simple algebraic identities, like x^2 = (-x)^2. Do not rely too much on it.

In[101]:=

Out[101]=

In[102]:=

Out[102]=

Created by Mathematica  (October 17, 2006)