Propositional logic.
¬(¬A∨B)).

This example is similar to the previous one. We play a saved play as example.

In[361]:=

F21 = Neg[Disj[Neg["A"], "B"]] ; Lin[F21] ;

In[363]:=

savedplay = ( "move 1" "Negation" ) ; ... "drop" Tarski[F21, "FontSize=18, TreeWidth=500", savedplay] ;

[Graphics:../HTMLFiles/index_49.gif]

[Graphics:../HTMLFiles/index_50.gif]

[Graphics:../HTMLFiles/index_51.gif]

\n\n

[Graphics:../HTMLFiles/index_53.gif]

[Graphics:../HTMLFiles/index_54.gif]

Abelard must defend the only subformula of ¬(¬A∨B)

Abelard moves: Negation

\n\n

[Graphics:../HTMLFiles/index_58.gif]

[Graphics:../HTMLFiles/index_59.gif]

Abelard must defend the left or right subformula of (¬A∨B)

Abelard moves: Left

\n\n

[Graphics:../HTMLFiles/index_63.gif]

[Graphics:../HTMLFiles/index_64.gif]

Eloise must defend the only subformula of ¬A

Eloise moves: Negation

\n\n

[Graphics:../HTMLFiles/index_68.gif]

[Graphics:../HTMLFiles/index_69.gif]

A is true.

Eloise moves: Atom

\n\n

[Graphics:../HTMLFiles/index_73.gif]

[Graphics:../HTMLFiles/index_74.gif]

Abelard has no subformulas to choose.

Abelard gives up.

[Graphics:../HTMLFiles/index_77.gif]

This is the list of all moves of the play:

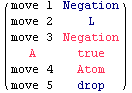
( move 1 Negation ) move 2 L move 3 Negation A true move 4 Atom move 5 drop

Created by Mathematica  (October 17, 2006)