A first order statement: integers are unbounded.
∀x.∃y.(x<y)

Consider the statement: ``for each integer x there is an integer y which is larger than x''. This statement is trivially true: just choose y=x+1. We can express it by the formula ∀x.∃y.(x<y). A winning strategy for this formula provides some map f selecting some y=f(x) such that x<f(x). A canonical winning strategy is associated to the map f(x)=x+1. Abelard attacks this formula by selecting, say, x=7. He claims that the subjudgement t.∃y.(7<y) of t.∀x.∃y.(x<y) is false. Eloise replays by selecting y=x+1=7+1=8 and defending the subjudgement t.7<8 of t.∃y.(7<y). This formula is indeed true. Abelard is forced to attack T, that is, is forced to move from t.T. Abelard cannot move and he gives up.

In[365]:=

In[366]:=

Out[366]=

We choose the parameter of the game and we play a saved game.

In[367]:=

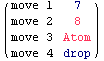
Created by Mathematica  (October 17, 2006)