x = h(h(x)+1) is an identity for no h:N→N.
∃x.x≠h(h(x)+1)
In[516]:=
![]()
In[517]:=
![]()
Out[517]=
![]()
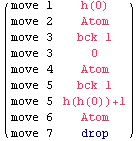
This is a simple, non-essential way of using backtracking, just a preliminary example. No matter what h is, the predicate x≠h(h(x)+1) is true either for some x in {h(0), 0, h(h(0)+1)} (we skip the proof). The winning strategy of Eloise consists in selecting the 3 values x=h(0), 0, h(h(0)+1), one after the other. The first time x≠h(h(x)+1) is true, Eloise wins. There are no moves of Abelard in this game. Backtracking allows Eloise to change her move of x. Eloise could by-pass, in this case, the use of backtracking, by computing first what is the right x, then selecting x just once.
Now we choose the parameters of the game and we play. During the play, whenever Eloise backtracks, say, from position 3 to position 1, we draw edges leading to positions 2, 3 thinner. This marks the fact that these position cannot any more be used in the play. Thick edges form the current Tarski play, which, for irreversible backtracking, is always the rightmost branch in the view-tree. In this section, backtracking is irreversible and whenever we backtrack to a position of index i we retract all positions of index >i. In this example, h(x) is the polynomial x*(x-1)
In[518]:=
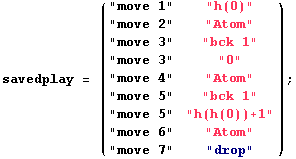
In[519]:=
![BCK[F26, "LCM, MaterialImplication, CutFree", "View-Tree, FontSize=18, TreeWidth=900", "Polynomial h(x)=x*(x-1)", savedplay]](../HTMLFiles/index_31.gif)
![[Graphics:../HTMLFiles/index_32.gif]](../HTMLFiles/index_32.gif)
![]()
![[Graphics:../HTMLFiles/index_34.gif]](../HTMLFiles/index_34.gif)
![]()
![[Graphics:../HTMLFiles/index_36.gif]](../HTMLFiles/index_36.gif)
![]()
![[Graphics:../HTMLFiles/index_38.gif]](../HTMLFiles/index_38.gif)
![]()
![[Graphics:../HTMLFiles/index_40.gif]](../HTMLFiles/index_40.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_51.gif]](../HTMLFiles/index_51.gif)
![]()
![[Graphics:../HTMLFiles/index_53.gif]](../HTMLFiles/index_53.gif)
![]()
![[Graphics:../HTMLFiles/index_55.gif]](../HTMLFiles/index_55.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_66.gif]](../HTMLFiles/index_66.gif)
![]()
![[Graphics:../HTMLFiles/index_68.gif]](../HTMLFiles/index_68.gif)
![]()
![[Graphics:../HTMLFiles/index_70.gif]](../HTMLFiles/index_70.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_82.gif]](../HTMLFiles/index_82.gif)
![]()
![[Graphics:../HTMLFiles/index_84.gif]](../HTMLFiles/index_84.gif)
![]()
![[Graphics:../HTMLFiles/index_86.gif]](../HTMLFiles/index_86.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_97.gif]](../HTMLFiles/index_97.gif)
![]()
![[Graphics:../HTMLFiles/index_99.gif]](../HTMLFiles/index_99.gif)
![]()
![[Graphics:../HTMLFiles/index_101.gif]](../HTMLFiles/index_101.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_112.gif]](../HTMLFiles/index_112.gif)
![]()
![[Graphics:../HTMLFiles/index_114.gif]](../HTMLFiles/index_114.gif)
![]()
![[Graphics:../HTMLFiles/index_116.gif]](../HTMLFiles/index_116.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_128.gif]](../HTMLFiles/index_128.gif)
![]()
![[Graphics:../HTMLFiles/index_130.gif]](../HTMLFiles/index_130.gif)
![]()
![[Graphics:../HTMLFiles/index_132.gif]](../HTMLFiles/index_132.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_143.gif]](../HTMLFiles/index_143.gif)
![]()
![[Graphics:../HTMLFiles/index_145.gif]](../HTMLFiles/index_145.gif)
![]()
![[Graphics:../HTMLFiles/index_147.gif]](../HTMLFiles/index_147.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_158.gif]](../HTMLFiles/index_158.gif)
![]()
![[Graphics:../HTMLFiles/index_160.gif]](../HTMLFiles/index_160.gif)
![]()
![[Graphics:../HTMLFiles/index_162.gif]](../HTMLFiles/index_162.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_172.gif]](../HTMLFiles/index_172.gif)
![]()
Created by Mathematica (October 20, 2006)