![Clear[f] ; F6 = Ex["x", Un["y", "f(x)≤f(y)"]] ; Lin[F6]](../HTMLFiles/index_175.gif)
Cut-free Positive LCM: each map over N has a minimum point.
∃x.∀y.f(x)≤f(y)
This example is taken from the introduction to games with irreversible backtracking. Let f:N→N. Eloise claims there is a minimum point of f, i.e., some x such that f(x)≤f(y) for all y in N. This can be expressed by ∃x.∀y.f(x)≤f(y). No such x can be computed uniformly on f: in general, in order to know whether f(x)≤f(y) for all y in N, there is no other way but computing the truth values of f(x)≤f(y) for all y in N, and this cannot be done in finite time.
Eloise wins the game by an essential use of backtracking. Eloise play a random value first, say, x=n0. If Abelard knows of some y=n1 such that f(n0) > f(n1), he plays n1 and (temporarily) wins. Eloise can backtrack to the moment she made the choice of x, and choose x=n1 this time. If Abelard knows of some y=n2 such that f(n1) > f(n2), he plays n1 and (temporarily) wins. And so forth. At each step, Eloise chooses, as next value of x, the previous value of y by Abelard. The result is some decreasing sequence f(n1) > f(n2) > f(n3) > ... . The only way Eloise can lose is by backtracking infinitely many times to the moment she chooses x. But this cannot be, because a sequence of nonnegative integers cannot decrease forever. At some step, we must have, say, f(n3) ≤ f(n4). In this moment, Abelard cannot find some y such that f(n3)>f(y), and he loses.
Remark that Abelard can lose either because there is no y such that f(n3)>f(y), or because there is some, but he is unable to find any. We cannot decide what is the case, this would be equivalent to compute the minimum point x.
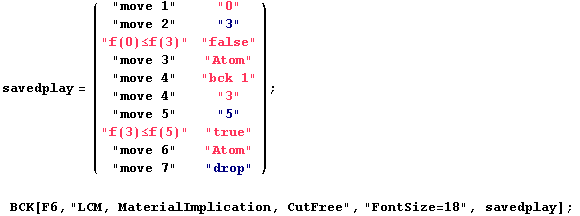
Now we choose the parameters of the game and we play. During the play, whenever Eloise backtracks, say, from position 4 to position 1, we draw the edges leading to positions 2, 3, 4 thinner. This marks the fact that these positions cannot any more be used in the play. Thick edges form the current Tarski play, which, for irreversible backtracking, is always the rightmost branch in the view-tree. In this section, backtracking is irreversible, and whenever we backtrack to a position of index i, we retract all positions of index >i.
In[520]:=
![Clear[f] ; F6 = Ex["x", Un["y", "f(x)≤f(y)"]] ; Lin[F6]](../HTMLFiles/index_175.gif)
Out[522]=
![]()
In[523]:=
![[Graphics:../HTMLFiles/index_178.gif]](../HTMLFiles/index_178.gif)
![]()
![[Graphics:../HTMLFiles/index_180.gif]](../HTMLFiles/index_180.gif)
![]()
![[Graphics:../HTMLFiles/index_182.gif]](../HTMLFiles/index_182.gif)
![]()
![[Graphics:../HTMLFiles/index_184.gif]](../HTMLFiles/index_184.gif)
![]()
![[Graphics:../HTMLFiles/index_186.gif]](../HTMLFiles/index_186.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_197.gif]](../HTMLFiles/index_197.gif)
![]()
![[Graphics:../HTMLFiles/index_199.gif]](../HTMLFiles/index_199.gif)
![]()
![[Graphics:../HTMLFiles/index_201.gif]](../HTMLFiles/index_201.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_212.gif]](../HTMLFiles/index_212.gif)
![]()
![[Graphics:../HTMLFiles/index_214.gif]](../HTMLFiles/index_214.gif)
![]()
![[Graphics:../HTMLFiles/index_216.gif]](../HTMLFiles/index_216.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_227.gif]](../HTMLFiles/index_227.gif)
![]()
![[Graphics:../HTMLFiles/index_229.gif]](../HTMLFiles/index_229.gif)
![]()
![[Graphics:../HTMLFiles/index_231.gif]](../HTMLFiles/index_231.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_243.gif]](../HTMLFiles/index_243.gif)
![]()
![[Graphics:../HTMLFiles/index_245.gif]](../HTMLFiles/index_245.gif)
![]()
![[Graphics:../HTMLFiles/index_247.gif]](../HTMLFiles/index_247.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_258.gif]](../HTMLFiles/index_258.gif)
![]()
![[Graphics:../HTMLFiles/index_260.gif]](../HTMLFiles/index_260.gif)
![]()
![[Graphics:../HTMLFiles/index_262.gif]](../HTMLFiles/index_262.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_273.gif]](../HTMLFiles/index_273.gif)
![]()
![[Graphics:../HTMLFiles/index_275.gif]](../HTMLFiles/index_275.gif)
![]()
![[Graphics:../HTMLFiles/index_277.gif]](../HTMLFiles/index_277.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_288.gif]](../HTMLFiles/index_288.gif)
![]()
![[Graphics:../HTMLFiles/index_290.gif]](../HTMLFiles/index_290.gif)
![]()
![[Graphics:../HTMLFiles/index_292.gif]](../HTMLFiles/index_292.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_302.gif]](../HTMLFiles/index_302.gif)
![]()
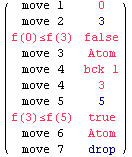
Out[523]=
![]()
Created by Mathematica (October 20, 2006)