A generic position of the play in sequent form.

Drawing a position in sequent form. We also represent a position with the list of judgements Eloise can backtrack to, with the negative judgements first.
                            f.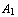A_1, ..., f.A_n,  t.B_1, ..., t.B_m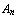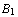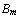
The positions Eloise can backtrack to are the nodes of the current Tarski play (of the branch ending in the golden ball). We read a sequent as: ``either 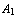A_1is false, or ..., or 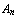A_n is false, or 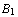B_1is true, or ..., or 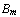B_mis true''. The same sequent can be read as: `if 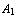A_1is true, and ..., and 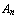A_n is true, then either 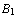B_1is true, or ..., or 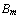B_mis true''. We write the same sequent also in the form:
                            A_1, ..., A_n |- B_1, ..., B_m
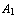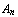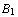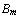
and we call it sequent-view (of Eloise). In the step 14 of the previous play, the sequent is:
            t.∀x.∃y.∀z.f(x,y)≤f(x,z),   t.∃y.∀z.f(a,y)≤f(a,z),   t.∀z.f(a,e)≤f(a,z),   t.f(a,e)≤f(a,e'),   t.T
or
            {} |- ∀x.∃y.∀z.f(x,y)≤f(x,z), ∃y.∀z.f(a,y)≤f(a,z), ∀z.f(a,e)≤f(a,z), f(a,e)≤f(a,e'), T        
We print boldface the current goal (the judgement marked by the golden ball in the view-tree).

What is the intuitive meaning of the Sequent-view? From a logical viewpoint, 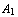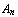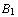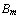A_1, ..., A_n |- B_1, ..., B_m is a complete description of the thesis of Eloise. The current position of the play is the instance of the thesis Eloise is currently defending (if it is a formula with a t. in front), or attacking (if it is a formula with a f. in front). If Eloise backtracks, she switches to some other formula from the same sequent, again defending it (if it is a formula with a t. in front), or attacking it (if it is a formula with a f. in front).

The sequent-view is formally defined for Abelard, too, even if Abelard cannot backtrack. The sequent-view of Abelard is the list of nodes of just the current Tarski play (of the branch ending in the golden ball). The role of f and t are reversed, though. Negative judgements are in the right-hand-side, and positive judgements in the left-hand-side.  In the step 14 of the previous play, the sequent is:
            f.∀x.∃y.∀z.f(x,y)≤f(x,z),   f.∃y.∀z.f(a,y)≤f(a,z),   ft.∀z.f(a,e)≤f(a,z),   f.f(a,e)≤f(a,e'),   f.T
or
            ∀x.∃y.∀z.f(x,y)≤f(x,z), ∃y.∀z.f(a,y)≤f(a,z), ∀z.f(a,e)≤f(a,z), f(a,e)≤f(a,e'), T     |- {}
We print boldface the current goal (the judgement marked by the golden ball in the view-tree).

Created by Mathematica  (October 20, 2006)