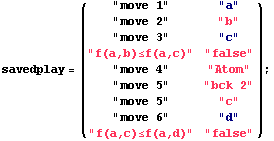
F31 = Un["x",Ex["y",Un["z", "f(x,y)≤f(x,z)"]]];
BCK[
F31,
"LCM, CutFree,MaterialImplication",
"View-Tree, FontSize=14,TreeWidth=800, Level-Height=70",
savedplay]
§2.2 How to use the program ``BCK''
Installing the program ``BCK''. You need Mathematica interpreter of Wolfram co. to install it. Select the title: ``A program implementing ...'', then press Shift+Enter and wait a few seconds.
Calling the program ``BCK''. The program is started by executing (i.e., by copying into a free location, then pressing Shift+Enter):
BCK[Formula, Arg1, Arg2, ... ]
What ``BCK'' does. You can play several kind of backtracking games for a given formula, drawing each position in tree form. If you want Tarski plays (no backtracking), no cut-rule, and Material Implication, add as argument the string: Intuitionistic, CutFree, MaterialImplication. If you want irreversible backtracking, no cut-rule, and Material Implication (as in this section), add as argument the string: LCM, CutFree, MaterialImplication.
Input form for formulas. Variables, terms, and atomic formulas are written between "...", for instance: "x", y", "x<y". Compound formulas are written using the operators: Conj[A,B], Disj[A,B], Impl[A,B], Neg[A], Un["x",A], Ex["x",A], denoting A∧B, A∨B, A⇒B, ¬A, ∀x.A, ∃x.A. For instance, ∀x.∃y.(x<y) becomes Un["x",Ex["y","x<y"]]. If F is in input form, you can recover the usual syntax for F executing Lin[F].
Graphic parameters. An extra argument can be a strings: par1, par2, par3=n, ..., where par1, par2, par3, ... are graphic parameters. If a parameter is not assigned, it is taken with the previous value. Graphic parameters include: FontSize=... (say: 12,14,18, ..). TreeWidth=... (in pixels). LevelHeight=... (height in pixels of each level of the tree). Two alternative parameters: View-Tree or TarskiPlay. The parameter View-Tree draws views, both in form of trees and in form of sequents, and for both players. The parameter TarskiPlay draws only the current Tarski play. You can merge all parameters in one long string, or divide them in more strings.
Language parameters. Predicates, constants and functions symbols include those of Mathematica. If you want to add generic symbols (without a definition), add as argument a string "Symbol s_1, ..., s_n". If you want to define functions f(x1,...,xn)=P(x1,...,xn) (with P any polynomial), or f(x1,...,xn)=t (with t any term of the language with variables all in x1,...,xn), or constants a=e (with e any closed term), add as argument a single definition: "Polynomial f(x1,...,xn)=P(x1,...,xn)" or "Term f(x1,...,xn)=t" or "Term a=e". If you want to define a logical constant C=A (with A a closed formula in input form) or P(x1,...,xn)=B (with B a formula in input form, with free variables all in x1,...,xn), execute (by Shif+Enter) before the command BCK the following command: SetAbbreviation["C",A] or SetAbbreviation["P(x1,...,xn)",B].
An example. Copy in a new location, then execute (by Shif+Enter) all the following expressions:
(* We add the abbreviation L(x,y) = (x<y∧f(x)≤f(y)) *)
SetAbbreviation["L(x,y)",Conj["x<y", "f(x)≤f(y)"]];
(* A formula in input form: ∃x.∃y.( L(x,y) ∧ ∃z. L(y,z) ) *)
F32=Ex["x",Ex["y",Conj["L(x,y)",Ex["z","L(y,z)"]]]];
(* The same formula in the usual syntax *)
Lin[F32]
(* Calling the program ``BCK'', with f(x)=x*(x-2)*(x-4)+5 *)
BCK[F32, "LCM, MaterialImplication, CutFree",
"TreeWidth=900,LevelHeight=70,FontSize=14",
"Polynomial f(x)=x*(x-2)*(x-4)+5"];
How the play runs. ``Tarski'' asks for a move the player who should move next. The player can answer: ``Left'',``Right'' for selecting the left- or right-hand side of a judgement t.A∧B, t.A∨B, t.A⇒B, or f.A∧B, f.A∨B, f.A⇒B; ``Negation'' to select the only subjudgement of a negation t.¬A or f.¬A; ``Atom'' for the only subformula of an atom t.a or f.a (t.T or f.T if a is true, and t.F or f.F is a is false) ; t (a closed term) for selecting the instance t.A[t/x] or f.A[t/x] of a quantification t.∀x.A, t.∃x.A, or f.∀x.A, f.∃x.A. Eloise can also backtrack from node i to any previous node j<i, typing ``bck j''. In this case nodes i+1, .., j are retracted (they are drawn thinner). Eloise cannot backtrack to a retracted move. There is only one branch with thick edges, is the branch ending in the golden ball denoting the current position. Eloise can only backtrack to some node of this branch. When the current node is an atomic formula A whose truth value is open, the program asks the player moving next for the truth value of A. The player should provide it in a consistent way.
Saved plays. An argument can be also a saved play, in matrix form.
Saved played in matrix form are available whenever a play ends. We can delete any number of lines at the end, save just an initial part of the play, then re-play just the initial part of the play. For instance, copy in a new location,then execute (Shif+Enter) all expressions below:
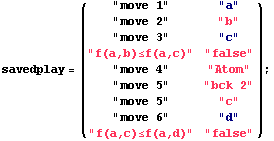
F31 = Un["x",Ex["y",Un["z", "f(x,y)≤f(x,z)"]]];
BCK[
F31,
"LCM, CutFree,MaterialImplication",
"View-Tree, FontSize=14,TreeWidth=800, Level-Height=70",
savedplay]
Created by Mathematica (October 20, 2006)