A generic position of the play in sequent form.

The sequent-view for games with irreversible and reversible backtracking are quite different. The reason is that the sequent-view of a position is defined in term of which backtracking is allowed from this position. The backtracking allowed from a given position is quite different in the two games.

Drawing a position in sequent form. We represent a position with the list of judgements Eloise can backtrack to, with the negative judgements first.
                            f.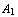A_1, ..., f.A_n,  t.B_1, ..., t.B_m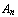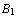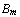
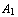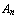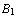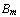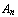The positions Eloise can backtrack to are all previous nodes, not just all nodes of the current Tarski play. We read a sequent as: ``either A_1is false, or ..., or A_n is false, or B_1is true, or ..., or B_mis true''. The same sequent can be read as: `if A_1is true, and ..., and A_n is true, then either B_1is true, or ..., or B_mis true''. We write the same sequent also in the form:
                            A_1, ..., A_n |- B_1, ..., B_m
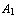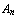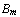
and we call it sequent-view (of Eloise). This is the sequent-view of Eloise, in the step 11 of the previous play (with the current goal printed boldface). It includes all formulas, even those which are temporarily retracted.

{P(a,b,c)} , ,  {}

⊢

{∀x.(∃y.∀z.P(x,y,z)∨∀y.∃z.星(x,y,z)), (∃y.∀z.P ... ∃z.星(a,b,z), ∃y.∀z.P(a,y,z), ∀z.P(a,b,z), P(a,b,c), , 星(a,b,c)}

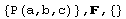
What is the intuitive meaning of the Sequent-view? From a logical viewpoint, 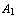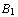A_1, ..., A_n |- B_1, ..., B_m is a complete description of the thesis of Eloise. The current goal is the instance of the thesis Eloise is currently defending (if it is a formula with a t. in front), or attacking (if it is a formula with a f. in front). If Eloise backtracks, she changes the instance of the thesis she is currently defending or attacking.

The sequent-view is formally defined for Abelard, too, even if Abelard cannot backtrack. The sequent-view of Abelard is the list of nodes of just the current Tarski play (of the branch ending in the golden ball). The role of f and t are reversed, though. Negative judgements are in the right-hand-side, and positive judgements in the left-hand-side. This is the sequent-view of Abelard, in the step 11 of the previous play (with the current goal printed boldface).

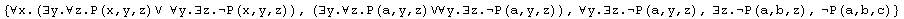
{∀x.(∃y.∀z.P(x,y,z)∨ ∀y.∃z.星(x,y,z)), (∃y.∀z. ... z)∨∀y.∃z.星(a,y,z)), ∀y.∃z.星(a,y,z), ∃z.星(a,b,z), 星(a,b,c)}

⊢

{P(a,b,c)} , ,  {}

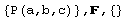
Created by Mathematica  (October 20, 2006)