Cut-free Positive Classical Logic: Excluded Middle for 2-quantifiers formulas.
∀x.(∃y.∀z.P(x,y,z)∨∀y.∃z.¬P(x,y,z))
P is any decidable predicate, and ∃y.∀z.P(x,y,z) is a generic degree 2 arithmetical formula. The game is associated to the formula ∀x.(∃y.∀z.P(x,y,z) ∨ ∀y.∃z .¬P(x,y,z)). This is an example of a game in which Eloise needs reversible backtracking to win using some effective strategy.
There is no effective winning strategy for Eloise in Tarski games. A winning strategy in Tarski games requires a map taking any value a for x, and returning the truth value of ∃y.∀z.P(a,y,z). If ∃y.∀z. P(a,y,z) is true, then Eloise must move t.∃y.∀z.P(a,y,z) to win. If ∃y.∀z.P(a,y,z) is false, then Eloise must move t.∀y.∃z.¬P(a,y,z)) to win. But there is no map deciding whether a generic degree 2 arithmetical formula is true or false.
There is no effective winning strategy for Eloise in games with irreversible backtracking. In a game with irreversible backtracking, Eloise can try to ``learn by trial-and-error'' whether ∃y.∀z.P(a,y,z) is true or false. But something goes wrong.
Eloise first assumes that ∃y.∀z.P(a,y,z) is false, and she moves t.∀y.∃z.¬P(a,y,z)), and defends it. Abelard attacks ∀y.∃z.¬P(a,y,z), by selecting some y=b, and moving t.∃z.¬P(a,b,z) is false. Now Eloise should find some z=c, such that ¬P(a,b,c) is true, that is, such that P(a,b,c) is false. But there could be no such c, or, even if there is some, Eloise could be unable to find it. The first part of the play is a dead end for Eloise.
Eloise now could backtrack from t.∃z.¬P(a,b,z) to the initial position t.∀x.(∃y.∀z.P(x,y,z) ∨ ∀y.∃z .¬P(x,y,z)). This time, she moves t.∃y.∀z.P(a,y,z), then t.∀z.P(a,b,z), claiming that P(a,b,z) is true for all z. Abelard could choose z=c, and moves t.P(a,b,c). If P(a,b,c) is false, then Abelard temporarily wins.
This is the crucial moment. Eloise would like to come back from the retracted position t.∃z.¬P(a,b,z), moving t.¬P(a,b,c) this time. This move is winning, because P(a,b,c) is, indeed, false. But coming back to t.∃z.¬P(a,b,z) requires to recover a retracted position. This can be done in a game with reversible backtracking. This cannot be done in a game with irreversible backtracking.
Is there any way Eloise could win using an effective strategy, and only irreversible backtracking? No, there is not. Let us reconsider the crucial moment, when Abelard moves t.P(a,b,c), and temporarily wins. Eloise can backtrack to the initial position t.∀x.(∃y.∀z.P(x,y,z) ∨ ∀y.∃z .¬P(x,y,z)), which has not been retracted. Then Eloise moves t.∀y.∃z.¬P(a,y,z)) again, hoping Abelard will choose y=b, and move t.∃z.¬P(a,b,z) again. In this case, Eloise moves t.¬P(a,b,c) and wins. But this is not always the case. This time, Abelard can choose y=b', and move t.∃z.¬P(a,b',z). Again, Eloise should find some z=c', such that ¬P(a,b',c') is true, that is, such that P(a,b,c') is false. But there could be no such c', or, even if there is some, Eloise could be unable to find it. Of course, Eloise can backtrack again, and again, but the same situation could arise infinitely many times. In this case Eloise loses, because she did an infinite backtracking.
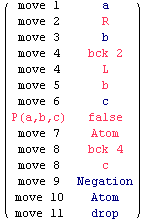
As we pointed out, there is, instead, an effective winning strategy for Eloise using reversible backtracking. Below we sketch it. Remark that, in the turn number 4, Eloise backtracks and retracts the node number 4, that is, the node t.∃z.¬P(a,b,z)). In the turn number 8, Eloise backtracks to the node number 4, recovering it. The move number 8 is the only move of the play requiring reversible backtracking. For Eloise, recovering the node number 8 is crucial in order to win. The program BCK prints a message saying:
![]()
Thin and thick edges in Eloise's view-tree (a reminder). Thick edges are the edges leading to a non-retracted node. Thick edges form the current Tarski play, that is, the branch of the view-tree leading to the current position of the play (the golden ball).
Now we choose the parameters of the game.
In[506]:=
![]()
In[507]:=
![]()
Out[507]=
![]()
In[508]:=
![]()
Out[508]=
![]()
In[509]:=
![savedplay = ( "move 1" "a" ) ; ... terialImplication, CutFree", "View-Tree, FontSize=18, TreeWidth=800", savedplay] ;](../HTMLFiles/index_38.gif)
![[Graphics:../HTMLFiles/index_39.gif]](../HTMLFiles/index_39.gif)
![]()
![[Graphics:../HTMLFiles/index_41.gif]](../HTMLFiles/index_41.gif)
![]()
![[Graphics:../HTMLFiles/index_43.gif]](../HTMLFiles/index_43.gif)
![]()
![[Graphics:../HTMLFiles/index_45.gif]](../HTMLFiles/index_45.gif)
![]()
![[Graphics:../HTMLFiles/index_47.gif]](../HTMLFiles/index_47.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_58.gif]](../HTMLFiles/index_58.gif)
![]()
![[Graphics:../HTMLFiles/index_60.gif]](../HTMLFiles/index_60.gif)
![]()
![[Graphics:../HTMLFiles/index_62.gif]](../HTMLFiles/index_62.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_73.gif]](../HTMLFiles/index_73.gif)
![]()
![[Graphics:../HTMLFiles/index_75.gif]](../HTMLFiles/index_75.gif)
![]()
![[Graphics:../HTMLFiles/index_77.gif]](../HTMLFiles/index_77.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_88.gif]](../HTMLFiles/index_88.gif)
![]()
![[Graphics:../HTMLFiles/index_90.gif]](../HTMLFiles/index_90.gif)
![]()
![[Graphics:../HTMLFiles/index_92.gif]](../HTMLFiles/index_92.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_104.gif]](../HTMLFiles/index_104.gif)
![]()
![[Graphics:../HTMLFiles/index_106.gif]](../HTMLFiles/index_106.gif)
![]()
![[Graphics:../HTMLFiles/index_108.gif]](../HTMLFiles/index_108.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_119.gif]](../HTMLFiles/index_119.gif)
![]()
![[Graphics:../HTMLFiles/index_121.gif]](../HTMLFiles/index_121.gif)
![]()
![[Graphics:../HTMLFiles/index_123.gif]](../HTMLFiles/index_123.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_134.gif]](../HTMLFiles/index_134.gif)
![]()
![[Graphics:../HTMLFiles/index_136.gif]](../HTMLFiles/index_136.gif)
![]()
![[Graphics:../HTMLFiles/index_138.gif]](../HTMLFiles/index_138.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_149.gif]](../HTMLFiles/index_149.gif)
![]()
![[Graphics:../HTMLFiles/index_151.gif]](../HTMLFiles/index_151.gif)
![]()
![[Graphics:../HTMLFiles/index_153.gif]](../HTMLFiles/index_153.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_164.gif]](../HTMLFiles/index_164.gif)
![]()
![[Graphics:../HTMLFiles/index_166.gif]](../HTMLFiles/index_166.gif)
![]()
![[Graphics:../HTMLFiles/index_168.gif]](../HTMLFiles/index_168.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_180.gif]](../HTMLFiles/index_180.gif)
![]()
![[Graphics:../HTMLFiles/index_182.gif]](../HTMLFiles/index_182.gif)
![]()
![[Graphics:../HTMLFiles/index_184.gif]](../HTMLFiles/index_184.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_195.gif]](../HTMLFiles/index_195.gif)
![]()
![[Graphics:../HTMLFiles/index_197.gif]](../HTMLFiles/index_197.gif)
![]()
![[Graphics:../HTMLFiles/index_199.gif]](../HTMLFiles/index_199.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_210.gif]](../HTMLFiles/index_210.gif)
![]()
![[Graphics:../HTMLFiles/index_212.gif]](../HTMLFiles/index_212.gif)
![]()
![[Graphics:../HTMLFiles/index_214.gif]](../HTMLFiles/index_214.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_225.gif]](../HTMLFiles/index_225.gif)
![]()
![[Graphics:../HTMLFiles/index_227.gif]](../HTMLFiles/index_227.gif)
![]()
![[Graphics:../HTMLFiles/index_229.gif]](../HTMLFiles/index_229.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_239.gif]](../HTMLFiles/index_239.gif)
![]()
Created by Mathematica (October 20, 2006)