Intuitionistic Logic: a prenex operation for ∃.
(∃x.P(x)∧∃y.Q(y))⇒∃x.∃y.(P(x)∧Q(y))
We already considered the same sample in the first section about constructive implication. We include a copy of the discussion here, in order to make this section self-contained.
Let A = ∃x.P(x) ∧ ∃y.Q(y) and B = ∃x'.∃y'.(P(x')∧Q(y')). A⇒B says we can always move ∃ outside ∧. The operational meaning of A⇒B is: there is an effective way of turning any evidence in favor of A into an evidence in favor of B. In this particular case, and evidence in favor of A is some vale x=a such that P(x), and some value y=b such that Q(b). An evidence in favor of B is a pair of values for x', y' such that P(z)∧Q(t). The obvious choice is taking x'=a, y'=b (we chose a trivial example on purpose).
We translate the informal argument above into a recursive winning strategy for Eloise, validating t.A⇒B.
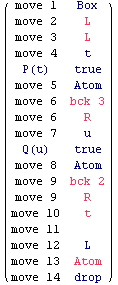
(move 1) The initial position is t.A⇒B (a conjunctive judgement).
(move 2) Abelard moves t.A⊃B.
(move 3) Eloise moves f.A, attacking the hypothesis A.
(move 4) Eloise moves f.∃x.P(x), attacking the left-hand side of A. (Normally, in a conjunction, Abelard would attack, but since there is an ``f.'' in front of A, roles are reversed, and Eloise attacks.) Abelard moves next, defending the truth of ∃x.P(x) (again, roles are reversed because there is an ``f.'').
(move 5) Abelard replies moving some f.P(t), and claiming P(t) is true. Eloise claims P(t) is false (again, roles are reversed because there is an ``f.'').
(move 6) Suppose P(t) is true. Then Abelard moves f.T and Eloise loses, but only temporarily.
(move 7) Eloise backtracks to f.A (position 3). She plays f.∃y.Q(y) this time.
(move 8) Abelard moves from f.∃y.Q(y), defending the truth of ∃y.Q(y) Therefore he replies choosing some f.Q(u), and claiming Q(u) is true.
(move 9) Suppose it is. Then Abelard moves f.T and Eloise loses. Eloise has lost twice in a row, but this was expected. The primary goal of Eloise on f.A is not to win. If she does, she wins the whole play, but she does not expect to win. The primary goal of Eloise is to obtain from Abelard some arguments in favor of A, that is, some t,u such that P(t), Q(u) are true. This is indeed the case.
(move 10) Eloise backtracks to t.A⊃B (the last positive judgement, position 2). This time, she moves t.B, a disjunctive judgement.
(move 11) Eloise moves t.∃y'.(P(t)∧Q(y')).
(move 12) Eloise moves t.P(t)∧Q(u).
(move 13) Abelard replies t.P(t). Now Abelard loses, because P(t) is true. Indeed,
(move 14) Eloise moves t.T, a true conjunctive atom. Abelard drops out (there are no ordinary moves, and Abelard cannot backtrack).
Remark that if Abelard, at step 13, moves t.Q(u), he loses as well, because Q(u) is true.
In[368]:=
![]()
In[369]:=
![]()
Out[370]=
![]()
Dotted positions (reminder). We mark with a big dot any position to which Eloise can backtrack to: all negative judgements of the tree, and the last positive judgement of the tree.
In[371]:=
![savedplay = ( "move 1" "Box" ) ; ... ructiveImplication, CutFree", "Symbol P, FontSize=18, TreeWidth=900", savedplay] ;](../HTMLFiles/index_250.gif)
![[Graphics:../HTMLFiles/index_251.gif]](../HTMLFiles/index_251.gif)
![]()
![[Graphics:../HTMLFiles/index_253.gif]](../HTMLFiles/index_253.gif)
![]()
![[Graphics:../HTMLFiles/index_255.gif]](../HTMLFiles/index_255.gif)
![]()
![[Graphics:../HTMLFiles/index_257.gif]](../HTMLFiles/index_257.gif)
![]()
![[Graphics:../HTMLFiles/index_259.gif]](../HTMLFiles/index_259.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_270.gif]](../HTMLFiles/index_270.gif)
![]()
![[Graphics:../HTMLFiles/index_272.gif]](../HTMLFiles/index_272.gif)
![]()
![[Graphics:../HTMLFiles/index_274.gif]](../HTMLFiles/index_274.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_285.gif]](../HTMLFiles/index_285.gif)
![]()
![[Graphics:../HTMLFiles/index_287.gif]](../HTMLFiles/index_287.gif)
![]()
![[Graphics:../HTMLFiles/index_289.gif]](../HTMLFiles/index_289.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_300.gif]](../HTMLFiles/index_300.gif)
![]()
![[Graphics:../HTMLFiles/index_302.gif]](../HTMLFiles/index_302.gif)
![]()
![[Graphics:../HTMLFiles/index_304.gif]](../HTMLFiles/index_304.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_315.gif]](../HTMLFiles/index_315.gif)
![]()
![[Graphics:../HTMLFiles/index_317.gif]](../HTMLFiles/index_317.gif)
![]()
![[Graphics:../HTMLFiles/index_319.gif]](../HTMLFiles/index_319.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_330.gif]](../HTMLFiles/index_330.gif)
![]()
![[Graphics:../HTMLFiles/index_332.gif]](../HTMLFiles/index_332.gif)
![]()
![[Graphics:../HTMLFiles/index_334.gif]](../HTMLFiles/index_334.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_346.gif]](../HTMLFiles/index_346.gif)
![]()
![[Graphics:../HTMLFiles/index_348.gif]](../HTMLFiles/index_348.gif)
![]()
![[Graphics:../HTMLFiles/index_350.gif]](../HTMLFiles/index_350.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_361.gif]](../HTMLFiles/index_361.gif)
![]()
![[Graphics:../HTMLFiles/index_363.gif]](../HTMLFiles/index_363.gif)
![]()
![[Graphics:../HTMLFiles/index_365.gif]](../HTMLFiles/index_365.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_376.gif]](../HTMLFiles/index_376.gif)
![]()
![[Graphics:../HTMLFiles/index_378.gif]](../HTMLFiles/index_378.gif)
![]()
![[Graphics:../HTMLFiles/index_380.gif]](../HTMLFiles/index_380.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_391.gif]](../HTMLFiles/index_391.gif)
![]()
![[Graphics:../HTMLFiles/index_393.gif]](../HTMLFiles/index_393.gif)
![]()
![[Graphics:../HTMLFiles/index_395.gif]](../HTMLFiles/index_395.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_407.gif]](../HTMLFiles/index_407.gif)
![]()
![[Graphics:../HTMLFiles/index_409.gif]](../HTMLFiles/index_409.gif)
![]()
![[Graphics:../HTMLFiles/index_411.gif]](../HTMLFiles/index_411.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_422.gif]](../HTMLFiles/index_422.gif)
![]()
![[Graphics:../HTMLFiles/index_424.gif]](../HTMLFiles/index_424.gif)
![]()
![[Graphics:../HTMLFiles/index_426.gif]](../HTMLFiles/index_426.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_437.gif]](../HTMLFiles/index_437.gif)
![]()
![[Graphics:../HTMLFiles/index_439.gif]](../HTMLFiles/index_439.gif)
![]()
![[Graphics:../HTMLFiles/index_441.gif]](../HTMLFiles/index_441.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_452.gif]](../HTMLFiles/index_452.gif)
![]()
![[Graphics:../HTMLFiles/index_454.gif]](../HTMLFiles/index_454.gif)
![]()
![[Graphics:../HTMLFiles/index_456.gif]](../HTMLFiles/index_456.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_467.gif]](../HTMLFiles/index_467.gif)
![]()
![[Graphics:../HTMLFiles/index_469.gif]](../HTMLFiles/index_469.gif)
![]()
![[Graphics:../HTMLFiles/index_471.gif]](../HTMLFiles/index_471.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_482.gif]](../HTMLFiles/index_482.gif)
![]()
![[Graphics:../HTMLFiles/index_484.gif]](../HTMLFiles/index_484.gif)
![]()
![[Graphics:../HTMLFiles/index_486.gif]](../HTMLFiles/index_486.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_496.gif]](../HTMLFiles/index_496.gif)
![]()
Created by Mathematica (November 11, 2006)