Intuitionistic Logic: if a satisfies ∀y.P(a,y), then a satisfies P(a,b)∧P(a,c).
(∃x.∀y.P(x,y)⇒∃x.(P(x,b)∧P(x,c)))
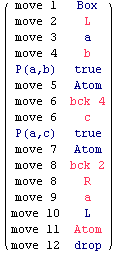
This example is similar to the previous one. Abelard moves t.∃x.∀y.P(x,y)⊃∃x.(P(x,b)∧P(x,c)), and Eloise replies f.∃x.∀y.P(x,y). In this initial part of the game, the goal of Eloise is not to win, but only to study how Abelard defends ∃x.∀y.P(x,y). Abelard has to move f.∀y.P(a,y) for some a, and defend ∀y. P(a,y). Thanks to backtracking, Eloise can attack f.∀y.P(a,y) twice in a row, first moving f.P(a,b), then moving f.P(a,c). The goal of Eloise, for the moment, is not win, but to check if, as Abelard claims, both P(a,b) and P(a,c) are true. If this is not the case, Abelard loses. If this is, indeed, the case, then Eloise knows that x=a is the correct move to defend t.∃x.(P(x,b)∧P(x,c). Therefore Eloise backtracks to t.∃x.∀y.P(x,y)⊃∃x.(P(x,b)∧P(x,c)). This time, she moves t.∃x.(P(x,b)∧P(x,c)), then t.P(a,b)∧P(a,c). Eventually, Eloise wins, because both P(a,b) and P(a,c) are true.
In[373]:=
![]()
In[374]:=
![]()
Out[375]=
![]()
Dotted positions (reminder). We mark with a big dot any position to which Eloise can backtrack to: all negative judgements of the tree, and the last positive judgement of the tree.
In[376]:=
![savedplay = ( "move 1" "Box" ) ; ... uot;Intuitionistic, ConstructiveImplication, CutFree", "FontSize=18", savedplay] ;](../HTMLFiles/index_502.gif)
![[Graphics:../HTMLFiles/index_503.gif]](../HTMLFiles/index_503.gif)
![]()
![[Graphics:../HTMLFiles/index_505.gif]](../HTMLFiles/index_505.gif)
![]()
![[Graphics:../HTMLFiles/index_507.gif]](../HTMLFiles/index_507.gif)
![]()
![[Graphics:../HTMLFiles/index_509.gif]](../HTMLFiles/index_509.gif)
![]()
![[Graphics:../HTMLFiles/index_511.gif]](../HTMLFiles/index_511.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_522.gif]](../HTMLFiles/index_522.gif)
![]()
![[Graphics:../HTMLFiles/index_524.gif]](../HTMLFiles/index_524.gif)
![]()
![[Graphics:../HTMLFiles/index_526.gif]](../HTMLFiles/index_526.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_537.gif]](../HTMLFiles/index_537.gif)
![]()
![[Graphics:../HTMLFiles/index_539.gif]](../HTMLFiles/index_539.gif)
![]()
![[Graphics:../HTMLFiles/index_541.gif]](../HTMLFiles/index_541.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_552.gif]](../HTMLFiles/index_552.gif)
![]()
![[Graphics:../HTMLFiles/index_554.gif]](../HTMLFiles/index_554.gif)
![]()
![[Graphics:../HTMLFiles/index_556.gif]](../HTMLFiles/index_556.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_567.gif]](../HTMLFiles/index_567.gif)
![]()
![[Graphics:../HTMLFiles/index_569.gif]](../HTMLFiles/index_569.gif)
![]()
![[Graphics:../HTMLFiles/index_571.gif]](../HTMLFiles/index_571.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_582.gif]](../HTMLFiles/index_582.gif)
![]()
![[Graphics:../HTMLFiles/index_584.gif]](../HTMLFiles/index_584.gif)
![]()
![[Graphics:../HTMLFiles/index_586.gif]](../HTMLFiles/index_586.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_598.gif]](../HTMLFiles/index_598.gif)
![]()
![[Graphics:../HTMLFiles/index_600.gif]](../HTMLFiles/index_600.gif)
![]()
![[Graphics:../HTMLFiles/index_602.gif]](../HTMLFiles/index_602.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_613.gif]](../HTMLFiles/index_613.gif)
![]()
![[Graphics:../HTMLFiles/index_615.gif]](../HTMLFiles/index_615.gif)
![]()
![[Graphics:../HTMLFiles/index_617.gif]](../HTMLFiles/index_617.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_628.gif]](../HTMLFiles/index_628.gif)
![]()
![[Graphics:../HTMLFiles/index_630.gif]](../HTMLFiles/index_630.gif)
![]()
![[Graphics:../HTMLFiles/index_632.gif]](../HTMLFiles/index_632.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_644.gif]](../HTMLFiles/index_644.gif)
![]()
![[Graphics:../HTMLFiles/index_646.gif]](../HTMLFiles/index_646.gif)
![]()
![[Graphics:../HTMLFiles/index_648.gif]](../HTMLFiles/index_648.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_659.gif]](../HTMLFiles/index_659.gif)
![]()
![[Graphics:../HTMLFiles/index_661.gif]](../HTMLFiles/index_661.gif)
![]()
![[Graphics:../HTMLFiles/index_663.gif]](../HTMLFiles/index_663.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_674.gif]](../HTMLFiles/index_674.gif)
![]()
![[Graphics:../HTMLFiles/index_676.gif]](../HTMLFiles/index_676.gif)
![]()
![[Graphics:../HTMLFiles/index_678.gif]](../HTMLFiles/index_678.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_689.gif]](../HTMLFiles/index_689.gif)
![]()
![[Graphics:../HTMLFiles/index_691.gif]](../HTMLFiles/index_691.gif)
![]()
![[Graphics:../HTMLFiles/index_693.gif]](../HTMLFiles/index_693.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_704.gif]](../HTMLFiles/index_704.gif)
![]()
![[Graphics:../HTMLFiles/index_706.gif]](../HTMLFiles/index_706.gif)
![]()
![[Graphics:../HTMLFiles/index_708.gif]](../HTMLFiles/index_708.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_718.gif]](../HTMLFiles/index_718.gif)
![]()
Created by Mathematica (November 11, 2006)