Intuitionistic Logic: Excluded Middle is not false.
∀x.¬¬(∃y.P(x,y)∨¬∃y.P(x,y))
In this example we check intuitionistic law of Excluded Middle: Excluded Middle is not false, or ∀x.¬¬(A∨¬A). We consider only the case A=∃y.P(x,y). Here is an intuitionistic proof. Fix any x, and assume ¬(A∨¬A), in order to prove F. We first prove a Claim: ¬A. Assume A in order to prove F. From the assumption A we deduce A∨¬A, and from the assumption ¬(A∨¬A) we deduce F. We just proved our Claim: ¬A. From the Claim ¬A we deduce A∨¬A. From the assumption ¬(A∨¬A), we conclude F.
The proof is rather subtle. It is not a mistake we proved ¬(A∨¬A) twice. Indeed, the first time we proved ¬(A∨¬A) from A in the proof of the Claim ¬A. The second time, we proved ¬(A∨¬A) from ¬A in the proof of ∀x.¬¬(A∨¬A).
There is a recursive winning strategy for Eloise (below we include a sample play). It is rather suble as well. Abelard moves t.¬¬(∃y.P(a,y)∨¬∃y. P(a,y)) for some a. Then Abelard moves f.¬(∃y.P(a,y)∨¬∃y.P(a,y)) (negation is considered conjunctive). Eloise moves t.(∃y.P(a,y)∨¬∃y.P(a,y)) (with an ``f.'' in front, negation is considered disjunctive). The first time, Eloise moves t.¬∃y.P(a,y). Then Abelard moves first f.∃y.P(a,y), claiming that ∃y.P(a,y) is false, then f.P(a,b) for some b. If this is indeed the case, Abelard wins, but only temporarily. Now Eloise knows how to defend ∃y.P(a,y). Eloise backtracks to f.¬(∃y.P(a,y)∨¬∃y.P(a,y)). This time, she moves t.∃y.P(a,y), then t.P(a,b), claiming that P(a,b) is true. This is indeed the case, and Eloise wins.
In[382]:=
![]()
Out[382]=
![]()
Dotted positions (reminder). We mark with a big dot any position to which Eloise can backtrack to: all negative judgements of the tree, and the last positive judgement of the tree.
In[383]:=
![savedplay = ( "move 1" "a" ) ; ... stic, ConstructiveImplication, CutFree", "TreeWidth=700,FontSize=18", savedplay] ;](../HTMLFiles/index_899.gif)
![[Graphics:../HTMLFiles/index_900.gif]](../HTMLFiles/index_900.gif)
![]()
![[Graphics:../HTMLFiles/index_902.gif]](../HTMLFiles/index_902.gif)
![]()
![[Graphics:../HTMLFiles/index_904.gif]](../HTMLFiles/index_904.gif)
![]()
![[Graphics:../HTMLFiles/index_906.gif]](../HTMLFiles/index_906.gif)
![]()
![[Graphics:../HTMLFiles/index_908.gif]](../HTMLFiles/index_908.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_919.gif]](../HTMLFiles/index_919.gif)
![]()
![[Graphics:../HTMLFiles/index_921.gif]](../HTMLFiles/index_921.gif)
![]()
![[Graphics:../HTMLFiles/index_923.gif]](../HTMLFiles/index_923.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_934.gif]](../HTMLFiles/index_934.gif)
![]()
![[Graphics:../HTMLFiles/index_936.gif]](../HTMLFiles/index_936.gif)
![]()
![[Graphics:../HTMLFiles/index_938.gif]](../HTMLFiles/index_938.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_949.gif]](../HTMLFiles/index_949.gif)
![]()
![[Graphics:../HTMLFiles/index_951.gif]](../HTMLFiles/index_951.gif)
![]()
![[Graphics:../HTMLFiles/index_953.gif]](../HTMLFiles/index_953.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_964.gif]](../HTMLFiles/index_964.gif)
![]()
![[Graphics:../HTMLFiles/index_966.gif]](../HTMLFiles/index_966.gif)
![]()
![[Graphics:../HTMLFiles/index_968.gif]](../HTMLFiles/index_968.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_979.gif]](../HTMLFiles/index_979.gif)
![]()
![[Graphics:../HTMLFiles/index_981.gif]](../HTMLFiles/index_981.gif)
![]()
![[Graphics:../HTMLFiles/index_983.gif]](../HTMLFiles/index_983.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_994.gif]](../HTMLFiles/index_994.gif)
![]()
![[Graphics:../HTMLFiles/index_996.gif]](../HTMLFiles/index_996.gif)
![]()
![[Graphics:../HTMLFiles/index_998.gif]](../HTMLFiles/index_998.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_1009.gif]](../HTMLFiles/index_1009.gif)
![]()
![[Graphics:../HTMLFiles/index_1011.gif]](../HTMLFiles/index_1011.gif)
![]()
![[Graphics:../HTMLFiles/index_1013.gif]](../HTMLFiles/index_1013.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_1025.gif]](../HTMLFiles/index_1025.gif)
![]()
![[Graphics:../HTMLFiles/index_1027.gif]](../HTMLFiles/index_1027.gif)
![]()
![[Graphics:../HTMLFiles/index_1029.gif]](../HTMLFiles/index_1029.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_1040.gif]](../HTMLFiles/index_1040.gif)
![]()
![[Graphics:../HTMLFiles/index_1042.gif]](../HTMLFiles/index_1042.gif)
![]()
![[Graphics:../HTMLFiles/index_1044.gif]](../HTMLFiles/index_1044.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_1055.gif]](../HTMLFiles/index_1055.gif)
![]()
![[Graphics:../HTMLFiles/index_1057.gif]](../HTMLFiles/index_1057.gif)
![]()
![[Graphics:../HTMLFiles/index_1059.gif]](../HTMLFiles/index_1059.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_1070.gif]](../HTMLFiles/index_1070.gif)
![]()
![[Graphics:../HTMLFiles/index_1072.gif]](../HTMLFiles/index_1072.gif)
![]()
![[Graphics:../HTMLFiles/index_1074.gif]](../HTMLFiles/index_1074.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_1085.gif]](../HTMLFiles/index_1085.gif)
![]()
![[Graphics:../HTMLFiles/index_1087.gif]](../HTMLFiles/index_1087.gif)
![]()
![[Graphics:../HTMLFiles/index_1089.gif]](../HTMLFiles/index_1089.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_1099.gif]](../HTMLFiles/index_1099.gif)
![]()
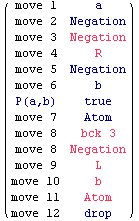
During the game, is essential for Eloise the possibility of backtracking to f.¬(∃y.P(a,y)∨¬∃y.P(a,y)) (a negative judgment). Look to the tree form of t.∀x.¬¬(∃y.P(x,y)∨¬∃y.P(x,y)). The position f.¬(∃y.P(a,y)∨¬∃y.P(a,y)) is the only position Eloise can backtrack to when she is in the position t.∃y.P(a,y), or the position t.¬∃y.P(a,y). Eloise cannot backtrack to t.∀x.¬¬(∃y.P(x,y)∨¬∃y.P(x,y)), nor to t.¬¬(∃y.P(a,y)∨¬∃y.P(a,y)), nor to t.(∃y.P(a,y)∨¬∃y.P(a,y)). Indeed, these positions are positive, and there is a positive position t.∃y.P(a,y) or t.¬∃y.P(a,y) which is closer. If Eloise cannot backtrack from t.∃y.P(a,y), or t.¬∃y.P(a,y) she loses. The reason is that, if Eloise cannot backtrack, then, when moving from t.(∃y.P(a,y)∨¬∃y.P(a,y)), she has to decide (in an irreversibly way, and uniformly in a) which is the best move between t.∃y.P(a,y) and t.¬∃y.P(a,y). The best move is t.∃y.P(a,y) if ∃y.P(a,y) is true, and it is t.¬∃y.P(a,y) if ∃y.P(a,y) is false. But the truth value of ∃y. P(a,y) cannot, in general, be computed uniformly in a. Instead, if Eloise can come back to f.¬(∃y.P(a,y)∨¬∃y.P(a,y)), then she replays t.(∃y.P(a,y)∨¬∃y.P(a,y)). In the next step, Eloise chooses again between t.∃y.P(a,y) and t.¬∃y.P(x,y). Choosing between t.∃y.P(x,y) and t.¬∃y.P(x,y) two times is exactly what Eloise needs to win, because she cannot make the best choice on her first try.
Created by Mathematica (November 11, 2006)