LCM: Weak Koenig's Lemma.
(∀x.∀y.(P(x)∨Q(y))⇒(∀x.P(x)∨∀y.Q(y)))
In[407]:=
![]()
We define the classical principle Weak Koenig's Lemma for recursive Lemma. We state it in the form: "if a recursive binary tree is infinite, then either the left or the right-hand side of the tree are infinite". Modulo choice axiom, this says that if a recursive binary tree is infinite, then it has an infinite branch. We get the branch by taking, at each step, left or right according to which side is infinite.
In[408]:=
![]()
In[409]:=
![]()
Out[409]=
![]()
Thin and thick edges in Eloise's view-tree (a reminder). Whenever we backtrack from position i to position j<i, we retract all positions j+1, ..., i. We mark this fact by drawing the edges leading to the positions j+1, ..., i thinner. If the position j was retracted, and now we recover it, the whole play comes back to the state it was in position j. We mark this fact by drawing the edges leading to positions 1, ..., j either thin or thick, according if they were thin or thick in the view-tree for position j. A single move can change the look of the view-tree deeply, because we can recover an older state of the tree.
Dotted positions (reminder). We mark with a big dot any position to which Eloise can backtrack to using intuitionistic backtracking: all negative judgements of the tree, and the last positive judgement, in the part of the tree having thick edges.
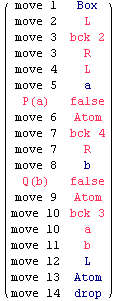
We choose the parameters of the game.
In[410]:=
![savedplay = ( "move 1" "Box" ) ; ... ;drop" BCK[F14, "LCM, ConstructiveImplication, CutFree, FontSize=18", savedplay] ;](../HTMLFiles/index_2161.gif)
![[Graphics:../HTMLFiles/index_2162.gif]](../HTMLFiles/index_2162.gif)
![]()
![[Graphics:../HTMLFiles/index_2164.gif]](../HTMLFiles/index_2164.gif)
![]()
![[Graphics:../HTMLFiles/index_2166.gif]](../HTMLFiles/index_2166.gif)
![]()
![[Graphics:../HTMLFiles/index_2168.gif]](../HTMLFiles/index_2168.gif)
![]()
![[Graphics:../HTMLFiles/index_2170.gif]](../HTMLFiles/index_2170.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2181.gif]](../HTMLFiles/index_2181.gif)
![]()
![[Graphics:../HTMLFiles/index_2183.gif]](../HTMLFiles/index_2183.gif)
![]()
![[Graphics:../HTMLFiles/index_2185.gif]](../HTMLFiles/index_2185.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2196.gif]](../HTMLFiles/index_2196.gif)
![]()
![[Graphics:../HTMLFiles/index_2198.gif]](../HTMLFiles/index_2198.gif)
![]()
![[Graphics:../HTMLFiles/index_2200.gif]](../HTMLFiles/index_2200.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2212.gif]](../HTMLFiles/index_2212.gif)
![]()
![[Graphics:../HTMLFiles/index_2214.gif]](../HTMLFiles/index_2214.gif)
![]()
![[Graphics:../HTMLFiles/index_2216.gif]](../HTMLFiles/index_2216.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2227.gif]](../HTMLFiles/index_2227.gif)
![]()
![[Graphics:../HTMLFiles/index_2229.gif]](../HTMLFiles/index_2229.gif)
![]()
![[Graphics:../HTMLFiles/index_2231.gif]](../HTMLFiles/index_2231.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2242.gif]](../HTMLFiles/index_2242.gif)
![]()
![[Graphics:../HTMLFiles/index_2244.gif]](../HTMLFiles/index_2244.gif)
![]()
![[Graphics:../HTMLFiles/index_2246.gif]](../HTMLFiles/index_2246.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2257.gif]](../HTMLFiles/index_2257.gif)
![]()
![[Graphics:../HTMLFiles/index_2259.gif]](../HTMLFiles/index_2259.gif)
![]()
![[Graphics:../HTMLFiles/index_2261.gif]](../HTMLFiles/index_2261.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2272.gif]](../HTMLFiles/index_2272.gif)
![]()
![[Graphics:../HTMLFiles/index_2274.gif]](../HTMLFiles/index_2274.gif)
![]()
![[Graphics:../HTMLFiles/index_2276.gif]](../HTMLFiles/index_2276.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2288.gif]](../HTMLFiles/index_2288.gif)
![]()
![[Graphics:../HTMLFiles/index_2290.gif]](../HTMLFiles/index_2290.gif)
![]()
![[Graphics:../HTMLFiles/index_2292.gif]](../HTMLFiles/index_2292.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2303.gif]](../HTMLFiles/index_2303.gif)
![]()
![[Graphics:../HTMLFiles/index_2305.gif]](../HTMLFiles/index_2305.gif)
![]()
![[Graphics:../HTMLFiles/index_2307.gif]](../HTMLFiles/index_2307.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2318.gif]](../HTMLFiles/index_2318.gif)
![]()
![[Graphics:../HTMLFiles/index_2320.gif]](../HTMLFiles/index_2320.gif)
![]()
![[Graphics:../HTMLFiles/index_2322.gif]](../HTMLFiles/index_2322.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2333.gif]](../HTMLFiles/index_2333.gif)
![]()
![[Graphics:../HTMLFiles/index_2335.gif]](../HTMLFiles/index_2335.gif)
![]()
![[Graphics:../HTMLFiles/index_2337.gif]](../HTMLFiles/index_2337.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2349.gif]](../HTMLFiles/index_2349.gif)
![]()
![[Graphics:../HTMLFiles/index_2351.gif]](../HTMLFiles/index_2351.gif)
![]()
![[Graphics:../HTMLFiles/index_2353.gif]](../HTMLFiles/index_2353.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2364.gif]](../HTMLFiles/index_2364.gif)
![]()
![[Graphics:../HTMLFiles/index_2366.gif]](../HTMLFiles/index_2366.gif)
![]()
![[Graphics:../HTMLFiles/index_2368.gif]](../HTMLFiles/index_2368.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2379.gif]](../HTMLFiles/index_2379.gif)
![]()
![[Graphics:../HTMLFiles/index_2381.gif]](../HTMLFiles/index_2381.gif)
![]()
![[Graphics:../HTMLFiles/index_2383.gif]](../HTMLFiles/index_2383.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2394.gif]](../HTMLFiles/index_2394.gif)
![]()
![[Graphics:../HTMLFiles/index_2396.gif]](../HTMLFiles/index_2396.gif)
![]()
![[Graphics:../HTMLFiles/index_2398.gif]](../HTMLFiles/index_2398.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2409.gif]](../HTMLFiles/index_2409.gif)
![]()
![[Graphics:../HTMLFiles/index_2411.gif]](../HTMLFiles/index_2411.gif)
![]()
![[Graphics:../HTMLFiles/index_2413.gif]](../HTMLFiles/index_2413.gif)
| Goal of: | Eloise |
![]()
![]()
![]()
| Goal of: | Abelard |
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_2423.gif]](../HTMLFiles/index_2423.gif)
![]()
Created by Mathematica (November 11, 2006)