An example of backtracking over ∃x.∀y.f(x)≤f(y) acceptable in no logic.

In[394]:=

Clear[f] ;

In[395]:=

Lin[F6]

Out[395]=

∃x.∀y.f(x)≤f(y)

In[396]:=

savedplay = ( "move 1" "3" ) ; &# ... )" "false" "move 5" "bck 3"

[Graphics:../HTMLFiles/index_2053.gif]

[Graphics:../HTMLFiles/index_2054.gif]

[Graphics:../HTMLFiles/index_2055.gif]

\n\n

[Graphics:../HTMLFiles/index_2057.gif]

[Graphics:../HTMLFiles/index_2058.gif]

[Graphics:../HTMLFiles/index_2059.gif]

[Graphics:../HTMLFiles/index_2060.gif]

[Graphics:../HTMLFiles/index_2061.gif]

Goal of: Eloise

{}

⊢

{} , ∃x.∀y.f(x)≤f(y),  {}

Goal of: Abelard

{} , ∃x.∀y.f(x)≤f(y),  {}

⊢

{}

____________________________________________________________________

Eloise must defend of some instance x of ∃x.∀y.f(x)≤f(y)

Eloise moves: x=3

\n\n

[Graphics:../HTMLFiles/index_2072.gif]

[Graphics:../HTMLFiles/index_2073.gif]

[Graphics:../HTMLFiles/index_2074.gif]

[Graphics:../HTMLFiles/index_2075.gif]

[Graphics:../HTMLFiles/index_2076.gif]

Goal of: Eloise

{}

⊢

{∃x.∀y.f(x)≤f(y)} , ∀y.f(3)≤f(y),  {}

Goal of: Abelard

{∃x.∀y.f(x)≤f(y)} , ∀y.f(3)≤f(y),  {}

⊢

{}

____________________________________________________________________

Abelard must attack some instance y of ∀y.f(3)≤f(y)

Abelard moves: y=5

\n\n

[Graphics:../HTMLFiles/index_2087.gif]

[Graphics:../HTMLFiles/index_2088.gif]

[Graphics:../HTMLFiles/index_2089.gif]

[Graphics:../HTMLFiles/index_2090.gif]

[Graphics:../HTMLFiles/index_2091.gif]

Goal of: Eloise

{}

⊢

{∃x.∀y.f(x)≤f(y), ∀y.f(3)≤f(y)} , f(3)≤f(5),  {}

Goal of: Abelard

{∃x.∀y.f(x)≤f(y), ∀y.f(3)≤f(y)} , f(3)≤f(5),  {}

⊢

{}

____________________________________________________________________

f(3)≤f(5) is true.

Eloise moves: Atom

\n\n

[Graphics:../HTMLFiles/index_2102.gif]

[Graphics:../HTMLFiles/index_2103.gif]

[Graphics:../HTMLFiles/index_2104.gif]

[Graphics:../HTMLFiles/index_2105.gif]

[Graphics:../HTMLFiles/index_2106.gif]

Goal of: Eloise

{}

⊢

{∃x.∀y.f(x)≤f(y), ∀y.f(3)≤f(y), f(3)≤f(5)} , ,  {}

Goal of: Abelard

{∃x.∀y.f(x)≤f(y), ∀y.f(3)≤f(y), f(3)≤f(5)} , ,  {}

⊢

{}

____________________________________________________________________

Abelard has no subformulas to choose.

Abelard backtracks to the node number 2 of the play.

This backtracking drops out the current goal and possibly more nodes (proper LCM move).

\n\n

[Graphics:../HTMLFiles/index_2118.gif]

[Graphics:../HTMLFiles/index_2119.gif]

[Graphics:../HTMLFiles/index_2120.gif]

[Graphics:../HTMLFiles/index_2121.gif]

[Graphics:../HTMLFiles/index_2122.gif]

Goal of: Eloise

{}

⊢

{∃x.∀y.f(x)≤f(y)} , ∀y.f(3)≤f(y),  {}

Goal of: Abelard

{∃x.∀y.f(x)≤f(y)} , ∀y.f(3)≤f(y),  {f(3)≤f(5), }

⊢

{}

____________________________________________________________________

Abelard must attack some instance y of ∀y.f(3)≤f(y)

Abelard moves: y=6

\n\n

[Graphics:../HTMLFiles/index_2133.gif]

[Graphics:../HTMLFiles/index_2134.gif]

[Graphics:../HTMLFiles/index_2135.gif]

[Graphics:../HTMLFiles/index_2136.gif]

[Graphics:../HTMLFiles/index_2137.gif]

Goal of: Eloise

{}

⊢

{∃x.∀y.f(x)≤f(y), ∀y.f(3)≤f(y)} , f(3)≤f(6),  {}

Goal of: Abelard

{∃x.∀y.f(x)≤f(y), ∀y.f(3)≤f(y), f(3)≤f(5), } , f(3)≤f(6),  {}

⊢

{}

____________________________________________________________________

f(3)≤f(6) is false.

Eloise backtracks to the node number 3 of the play.

This backtracking recovers a non-visible node (irregular move).

Eloise does a move not allowed in the logic: Classical with Cut rule. Eloise loses.

[Graphics:../HTMLFiles/index_2149.gif]

This is the list of all moves of the play:

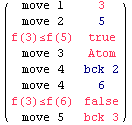
( move 1 3 ) move 2 5 ... move 4 6 f(3)≤f(6) false move 5 bck 3

Out[396]=

Null^2

Created by Mathematica  (November 11, 2006)