Capitolo 1. Sistemi lineari.
In questo testo, i numeri degli esercizi fanno riferimento al testo:
Esercizi di Geometria e Albegra Lineare I
di E. Abbena, G.M. Gianella.
Esercizio 1 del Capitolo 1 (Abbena-Gianella).
Risolvere il sistema:
| x1 + x2 - x3 = 1 |
| 2 x1 + 2 x2 + x3 = 0 |
| x1 + x2 + 2 x3 = -1 |
Suggerimenti. Definire una matrice A dei coefficienti, due vettori X delle variabili e B dei coefficienti. Disegnare per controllo (usare MatrixForm) A, X, AX, B. Indicare il prodotto di matrici con "A.X"). Risolvete A.X=B con Solve[A.X == B, {x1,x2,x3}] (omettiamo i casi particolari) oppure con Reduce[A.X == B, {x1,x2,x3}] (dà la soluzione completa).
Per il sistema in esame, molto semplice, sia Solve che Reduce forniscono tutte le soluzioni. In generale, invece, Reduce è più completo: per esempio trova anche le soluzioni nei casi in cui un coefficiente dipendente da parametri sia zero.
Attenzione (1). Definite X, B o entrambe come i vettori {x1,x2,x3}, {b1,b2,b3} (in questo caso, A.X e B sono vettori), oppure entrambe come matrici ridotte a un'unica colonna:
X = 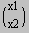 , B =
, B = 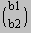
Equivalentemente:
X={{x1},{x2},{x3}}, B={{b1},{b2},{b3}}
In questo caso, A.X e B sono matrici.
Non potete invece scegliere X come vettore e B come matrice, o viceversa. In Mathematica non è possibile eguagliare un vettore ad una matrice-colonna, anche se della stessa dimensione.
Attenzione (2).Evitate inoltre definizioni del tipo
A = MatrixForm[...]
MatrixForm infatti produce il disegno di una matrice, non una matrice vera e propria. Non è possibile risolvere una equazione A.X ==B quando A è un disegno.
In[271]:=

In[272]:=
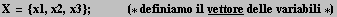
In[273]:=
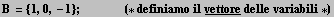
In[274]:=
![MatrixForm[A] MatrixForm[X] MatrixForm[A . X] MatrixForm[B]](../HTMLFiles/index_6.gif)
Out[274]//MatrixForm=
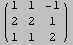
Out[275]//MatrixForm=
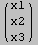
Out[276]//MatrixForm=
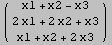
Out[277]//MatrixForm=
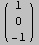
Per discutere la soluzione, calcolare Det[A].
Se Det[A] risulterà diverso da 0, la soluzione sarà unica.
Se Det[A] risulterà uguale a 0, le soluzioni potranno essere un insieme vuoto, oppure uno spazio vettoriale di dimensione 1 o più. La dimensione dello spazio delle soluzioni esprime il numero di parametri da cui la soluzione dipende. Si può calcolare calcolando la forma ridotta di A (comando RowReduce), e contando il numero delle righe tutte uguali a 0 ottenute. Questo procedimento funziona solo con matrici quadrate.
In[278]:=
![Det[A]](../HTMLFiles/index_11.gif)
Out[278]=
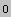
In[279]:=
![MatrixForm[RowReduce[A]]](../HTMLFiles/index_13.gif)
Out[279]//MatrixForm=
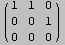
Infine, risolvere l'equazione A.X=B. In questo caso, i comandi Solve e Reduce danno lo stesso insieme di soluzioni. Controllare che la dimensione dello spazio delle soluzioni ottenuto sia quella prevista.
In[280]:=
![Solve[A . X == B, X] Reduce[A . X == B, X]](../HTMLFiles/index_15.gif)

Out[280]=
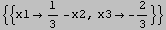
Out[281]=
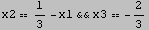
Esercizio 7 del Capitolo 1 (Abbena-Gianella).
Created by
Mathematica
(August 4, 2004)

![MatrixForm[A] MatrixForm[X] MatrixForm[A . X] MatrixForm[B]](../HTMLFiles/index_6.gif)